Correspondences for my image
Correspondences for the George Clooney Image
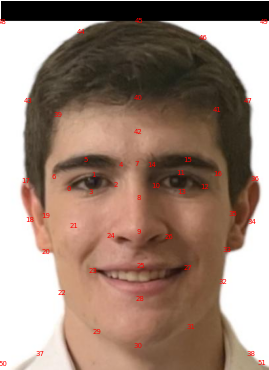
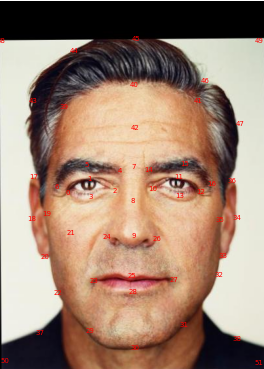
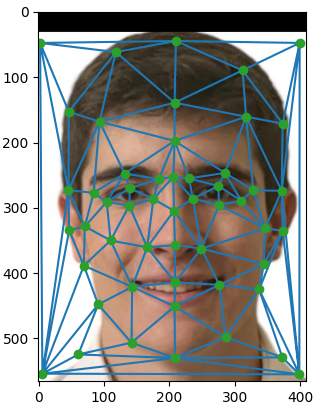
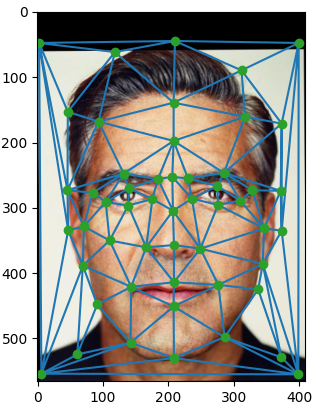
For this part, I used the provided tool from last year to define correspondence points in both images. Then I used Delaunay to create appropriate triangulations.
This was in my option the most challenging section of the project. As described in the problem statement, we must first warp both faces to the average shape and then averaging the colors together. However, looking forward to section 3, this is just a particular example of the morph function, with both coefficients = 0.5.
To do this, we iterate through each of the triangles in our Delaunay triangulation. In each iteration, we must calculate the values of the pixels of the destination from the source triangle. By solving a linear system, we find the affine matrix that describes the transformation from one triangle to the other. Then, we map the pixel values using bilinear interpolation.
The next part is based around the objective of creating a smooth transition from one image to another. To do this, we use a very similar approach to that of part 2. Now however, we use the parameters warp_frac and dissolve_frac to accomplish images which are closer to one image than the other. By making both parameters increase slowly, we achieve the desired smooth transitiion.
In the following section, we explore how to create the average face of a population, and then morph using that face. For this part I used the FEI face database provided in the project assignment. To do this, we first established the average correspondence points of the dataset and Delaunay triangulation. Then we reuse code from part 2 to morph each face into the average shape. Finally, we average the morphed images to obtained the desired average face. Note that for better results I added correspondence points in the corners for all images.
In order to warp my face to the average population's, I redefined the correspondence points so that they matched those of the original images. That is, the same number of points in corresponding locations. Using this method, I obtained the following results:
The reason why the face is deformed is because of inaccuracy in correspondence selection, and image cropping choice.
In this section, I create caricatures of my face by extrapolating from the population mean that I calculated in the last step. By using an extrapolation factor to alter the destination correspondaces I achieve different levels of caricaturization. In one direction:
In the other:
Note that if we were to set the factor to 1, we would get the original image back.
For my mandatory bells and whistles, I decided to morph my face into that of the average Bollywood actress. The target is of different sex and race so we expect funny results. Here are the original images:
I attempted to first compute the midway shape, and then only change color and shape:
Despite the rather distrubing shape image, we can see that my lips became smaller, my eyes turned inwards and my jaw became more round. Similarly, the color-only change keeps my features, but turns them into a strange female version. Spooky!